The Arrow Calculus
Lindley, Sam, Philip Wadler, and Jeremy Yallop
Journal of Functional Programming 20, no. 1 (2010): 51-69
https://doi.org/10.1016/j.entcs.2011.02.018
“Formally, arrows are defined by extending simply typed lambda calculus with three constants satisfying nine laws. And here is where the problems start. While some of the laws are easy to remember, others are not. Further, arrow expressions written with these constants use a “pointless” style of expression that can be hard to read and to write. (Not to mention that “pointless” is the last thing arrows should be.)
Fortunately, Paterson introduced a notation for arrows that is easier to read and to write, and in which some arrow laws may be directly expressed (Paterson 2001). But for all its benefits, Paterson’s notation is only a partial solution. It simply abbreviates terms built from the three constants, and there is no claim that its laws are adequate for all reasoning with arrows. Syntactic sugar is an apt metaphor: it sugars the pill, but the pill still must be swallowed.”
Wickham, Hadley
Journal of statistical software 59 (2014): 1-23.
LeCun, Yann, Yoshua Bengio, and Geoffrey Hinton
Nature 521, no. 7553 (2015): 436-444.
Bennett, Charles H., Gilles Brassard, and N. David Mermin
Physical Review Letters 68, no. 5 (1992): 557
Minsky, Marvin
Communications of the ACM 43, no. 8 (2000): 66-73
Turing, Alan
Proceedings of the London mathematical society 2, no. 1 (1937): 230-265
Lloyd, Seth
Nature 406, no. 6799 (2000): 1047-1054
Knuth, Donald E.
The Computer Journal 27, no. 2 (1984): 97-111
Brooks, Frederick P.
IEEE Computer 20, no. 4 (1987): 10-19
Lamport, Leslie, Robert Shostak, and Marshall Pease
ACM Transactions on Programming Languages and Systems (TOPLAS) 4, no. 3 (1982): 382–401
Lindley, Sam, Philip Wadler, and Jeremy Yallop
Journal of Functional Programming 20, no. 1 (2010): 51-69
Wadler, Philip
ACM SIGPLAN Notices 47, no. 9 (2012): 273-286










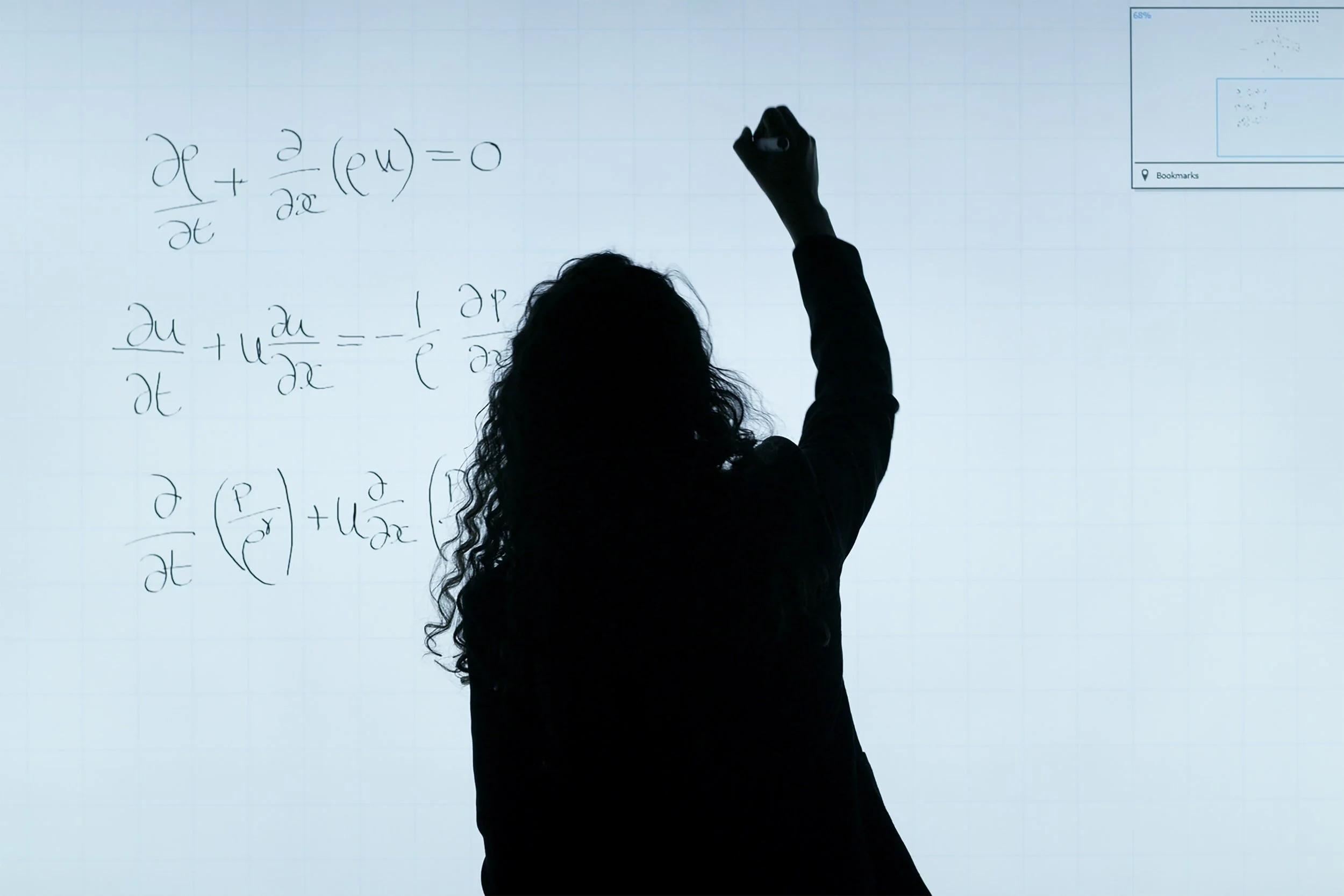
Richards, Blake A., Timothy Lillicrap, et al.
Nature Neuroscience 22, no. 11 (2019): 1761-1770.